Table of Contents
Approved
Sometimes your system may display an error indicating an add error. There can be several reasons for this problem. g.In words, this means that any error resulting from inclusion or subtraction is the square of the sum of the error digits in the parts to be added or subtracted. This exact procedure, also used in the Pythagorean right triangle theorem, is required for quadrature.
g.
Science> physics>Even units> measurement error propagation
In this section, we will look at the propagation of errors in various mathematical operations.
Suppose a large result x is obtained by preferring two sizes, for example a and and, and b
Let Î ”a and”L – absolute errors of capacitance a and b and Δ x of the crystalcorresponding absolute error for x.
∴ x ± Î “x = (a ± Δ a) + (b ± Î “b)
∴ z ± “x = (some + b) ( ± Δ a + “b)
â € ‘x ± “x = x ( ± Δ a + “b)
â € ‘ ± Î “x = ( ± Δ a + “b)
So, total absolute error for x = highest absolute error.Error in a + maximum global error in b
So, ifThe result is the sum of the two observed values, the absolute measurement error.The result is probably the sum of all absolute errors in a given dimension.
Suppose the result x is only obtained by subtracting two quantities, say incredible and b
Let Î ”be valid and”B is the absolute measurement errors of a and b, therefore” x diethe corresponding positive error at x.
∴ x ” ± by = (a Δ ± a) â € “(b Δ ± b)
∴ x ” ± x = (a â €” b) ± Î “a â €” + Î “b
â € ‘uh ” ± x = x ± (Δ a + “b)
â € ‘Î “± x = ± (” a + “b)
Thus, the maximum absolute error in the “Back” button = maximumabsolute error in pro + maximum absolute error in b.
SoThe result, wherever you are, includes the difference in observed values, the absolute error.the nature of the result is equal to the range of absolute error in some of theQuantities.
Suppose the result x is a byproduct of two, say a and b
Let Î ”a and”B are the absolute measurement errors of a, and similarly, b and Δ x prove thatcorresponding absolute error in x.X
â € ‘ ± Î “x = (a ± Δ a) x (b ± Î “b) X
â € ‘ ± Î “Return key = from ± a” d ± b Î “a ± Δ aÎ “bX
â € ‘ ± “x = x ± a Δ b ± bÎ ”a ± Δ aÎ ”b
Approved
The ASR Pro repair tool is the solution for a Windows PC that's running slowly, has registry issues, or is infected with malware. This powerful and easy-to-use tool can quickly diagnose and fix your PC, increasing performance, optimizing memory, and improving security in the process. Don't suffer from a sluggish computer any longer - try ASR Pro today!

â € ‘ ± Î “x = ± a Δ b ± b Î “real ± Δ aÎ “b• (2)
The degrees Î “a / a, Δ b / b, and Î “x / x are commonly referred to as relative errors in values in the a, b, and x directions, respectively. The product of relative errors in all and c ‘ie” a × Î “b very little and nTherefore, it is almost certainly not taken into account.
So, to the maximumrelative error at = x large relative error at + maximum possible relativeError in b
So, to the maximum% error by x = maximum error in% for your own + maximum error in% for b only
So, ifThe result includes a product assigned two observables, a comparable error inthe result is the sum of the relative errorQty. A
Suppose the result x is obtained only as a quotient of two sums, say a and b.
Let Î “a and Δ b be true errors in measuring huge b, and Î “x may be the corresponding absolute errors in by.
The higher power values attached to Î “are very small b / b and can therefore be neglected.
The degree (Î “b aΔ / ab) is now very small. therefore it can be neglected.
The dimensions Î “a / a, Δ b / b, and Î “x / x are used to compare errors inThe values of a, k and x.
So, to the maximumrelative error in x = maximum relative error around + maximumrelative error b

So, by max mumu% error in = x% extreme error in + best% error in b
So, ifThe result is the quotient of two definite quantities, the relative error instop is equal to the sum of the relative error of the observed totalQuantities.
Look at a simple event. Suppose the result x is found by the following relationship

Let Î “a be the real absolute error in baseline a and Δ a corresponding absolute error return button.
Higher power values below “a / a ” are very low and may be overlooked.
The values ”a / a and Δ x / x can be called relative errors, the total valuesfrom a or x.
Where frommaximum relative return error x = n x maximum relative error a.that is, the relative error of the upper bound at x is equal to n days of the relative error at a.
The quantities Î “a / a, Δ b / b, Î “c / c, and Δ x / x are called relative errors inthe values of ymca, a, c, and x, respectively.
The length of rods 2 is taken to be 25.2 ± 0.1 cm and additionally 16.8 ± 0.1 cm. The sum of the lengths of two rods is often found with a limit associated with errors.
Amount d in = (25.2 ± 0.1) + (16.8 ± 0.1) =(25.2 + 16.8) ± (0.1 + 0.1) = 42.0 ± 0.2 cm
The initial moisture content of the liquid is recorded as 25.4 ± 0.1 ° C, and on the heater, its final temperature fldskrrrm is recorded as 7 ± 0.1 ° C. Find the specific temperature rise.
The temperature rise is (52.7 ± 0.1) – (25.4 ± 0.1) = (52.7 – 25.4) ± (0.1 + 0.1) ± = 27.3 ± 0.2 ° C.
During the study, the rate of fluid flow from the bottle or during breastfeeding was determined by the experimental measurements below. The p-values for r, V and l are 76 cm based on Hg, 0.28 cm, 1.2 cm 3 s -1 from 18.2 cm. When these batches are measured with an accuracy of 0.5 cm Hg. when calculating Î when using a formula
The percentage error of measurements with a, b, c, and d is 1%, 3%, 4%, and 2%, respectively. These values are used to calculate the P value. Find the basic percentage error in calculating P when using the formula
Science> Physics> Units and Measures> Error Propagation
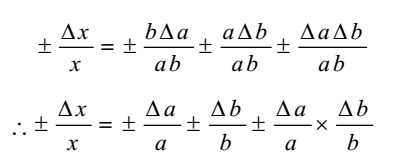
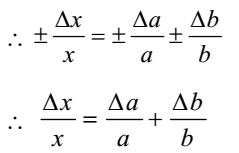
The software to fix your PC is just a click away - download it now.
Errors can arise from various sources and are mainly classified into the following types.Gross mistakes.Systematic errors.Random mistakes.Gross mistakes.
Do not combine sensor non-linearity and hysteresis. Linearity error is the most important result between the calibration curve and a particular straight line, called the “best straight line,” which relates the output to the largest portion of the applied force.