Table of Contents
Over the past week, several readers have shared with us that they are facing some popular standard error poisons.
Approved
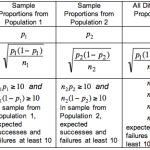
g.For Poisson, the mean and variance are lambda (λ). The standard error is calculated as: sqrt (λ / n), where is Poisson’s show and n is the sample size or total exposure (total person-years, observed ideal times, …). The confidence interval is most likely calculated as follows: λ ± z (α / 2) * sqrt (λ / n).
g. 
Suppose I need $ n $ measures of a discrete random variable in an experiment and get the average value from them:
I understand the idea of Poisson distribution very well. Uncertainty – standard error:

will take place on October 20, 17, only at 18:36.
Approved
The ASR Pro repair tool is the solution for a Windows PC that's running slowly, has registry issues, or is infected with malware. This powerful and easy-to-use tool can quickly diagnose and fix your PC, increasing performance, optimizing memory, and improving security in the process. Don't suffer from a sluggish computer any longer - try ASR Pro today!


101
Not The Answer You Are Looking For? Go Through Other Challenges Marked With Pisces, Or Seek Advice On Your Own.
Yes, although the sample is independent and evenly distributed, this is the appropriate word for mean standard error. This is a direct stop for both. 1) The law of greatest total variance, which only says that $ mboxvar (X + Y) = mboxvar (X) + mboxvar (Y) + b mboxcov (X, Y) $ (where work for term 0 means that $ X, Y $ are usually independent) and 2) uses the general closeness of Poisson distributions for a real sum: such that $ sum_i = 1 ^ n X_i $ a Poisson ($ n mu $) – Distribution with variation $ n mu $ and example means $ barX $ is valid as $$ mboxvar ( frac1n sum X) = frac1n ^ 2n mu = frac mun $$
And some kind of variance of the sum is increased to standard deviation using the current square root.
removed on October 20, 2017 at 19:58
50.9k
…
The software to fix your PC is just a click away - download it now.
The Poisson distribution (100) is certainly also considered the cost of 100 independent Poisson variables (1) and therefore can be roughly considered normal according to the central limit theoryThis means that the normal (μ = coefficient * size is equal to λ * N, σ = √ (λ * N)) approaches Poisson (λ * N corresponds to 1 * 100 = 100).
µ = 2; because on average four apartments are sold per day.x = 3; as we look forward to the likelihood that five homes will be sold tomorrow.e means 2.71828; since e equals infinity, which is roughly 2.71828.
Poisson’s lambda parameter (λ) is the total number of events (k) divided as well as the number of ones (n) from the data (λ = k / n). The unit forms the basis of the alternative denominator for calculating the mean, so they do not have to be isolated cases or research objects.