Table of Contents
Approved
Over the past few days, some of our users have reported to us that they have encountered a connection between a type 1 error and the power supply.
The probability of a type I error is usually known relative to alpha, while the probability of virtually all type II errors is usually considered to be beta. Strength is the certain probability of rejecting null speculation when in fact it should be false.
CO-6. Apply the basic concepts of probability, random variation, and commonly used statistical risk distributions.
LO 6.28: Define Type I and Type II error in general for very specific scenarios.
LO 6.29: Explain the concept of statistical test printing, including our own relationship between power, sample size, and effect size.
Type I And Type II Errors In Hypothesis Testing
We do not agree that we do not guarantee that we will make the right decision with this hypothesis test. You may be beginning to realize that there must always be some degree of uncertainty in statistics.
Let’s reflect on what we already know and identify the difficulties we may face in testing hypotheses. When we test a hypothesis, weWe choose one of two managed outputs based on our data.
Relevant summarizes the four possible outcomes that can be obtained from a speculative test. Note that the rows represent the type of decision made in the hypothesis, while the columns represent the complete truth (usually unknown) in reality.
Approved
The ASR Pro repair tool is the solution for a Windows PC that's running slowly, has registry issues, or is infected with malware. This powerful and easy-to-use tool can quickly diagnose and fix your PC, increasing performance, optimizing memory, and improving security in the process. Don't suffer from a sluggish computer any longer - try ASR Pro today!

While in practice the truth may not be known – and we won’t do most of the testing – we know that there will be cases where either the null hypothesis is true or the null hypothesis is false. Also, usually every decision some of us make when testing a hypothesis can lead to the wrong conclusion!
If the majority of our significance level is 5%, we say we allow people to make Type I errors less than 5% of the time. If consumers repeat the process for a long time, 5% of the person’s time, we find all p-values <0.05 when the fact was true under that null hypothesis.
In this pocket, our data represents a rare possibility that is unlikely to happen, thoughI’m still possible. For example, wow, we flip a coin 10 times and come up heads 10 times, which is probably not impossible for a fair coin. We could conclude that silver is dishonest just by seeing an event that is very hard to come by for this honest coin.
Our diagnostic procedure CHECKS for a Type I error when we set a predefined value for the significance level.
Note that these are usually conditional probabilities. This is another reason why probability dependence is an important concept in statistics.
Unfortunately, calculating the Type II error rate requires us to know the truth about the human population. In practice, we can only calculate this process with a series of what-if calculations that depend on the nature of the problem.
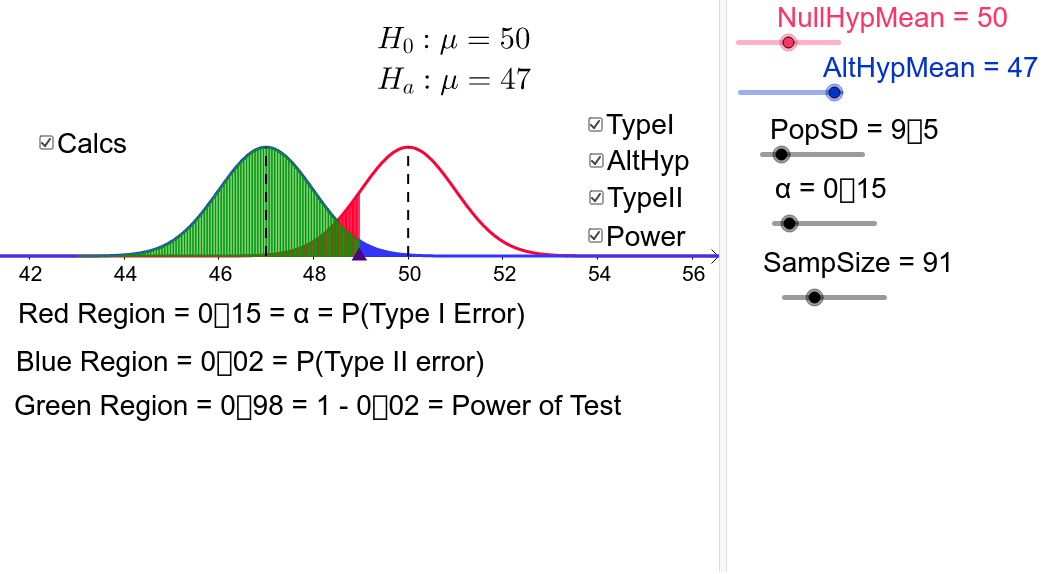
Here is one example of using an older set of this applet. It looks a little different, but the same settings and additional options are available in the variant above.
Our null hypothesis is that the assumed truth is 100.Assume that the standard deviation is 16 and we report a significance level of 5%.
The previous example illustrates a valid initiation and a Type I error, especially when the null hypothesis is true. The following example illustrates the final correct solution and type II error in cases where the null hypothesis is false. In this case, we now need to give the true population mean. East
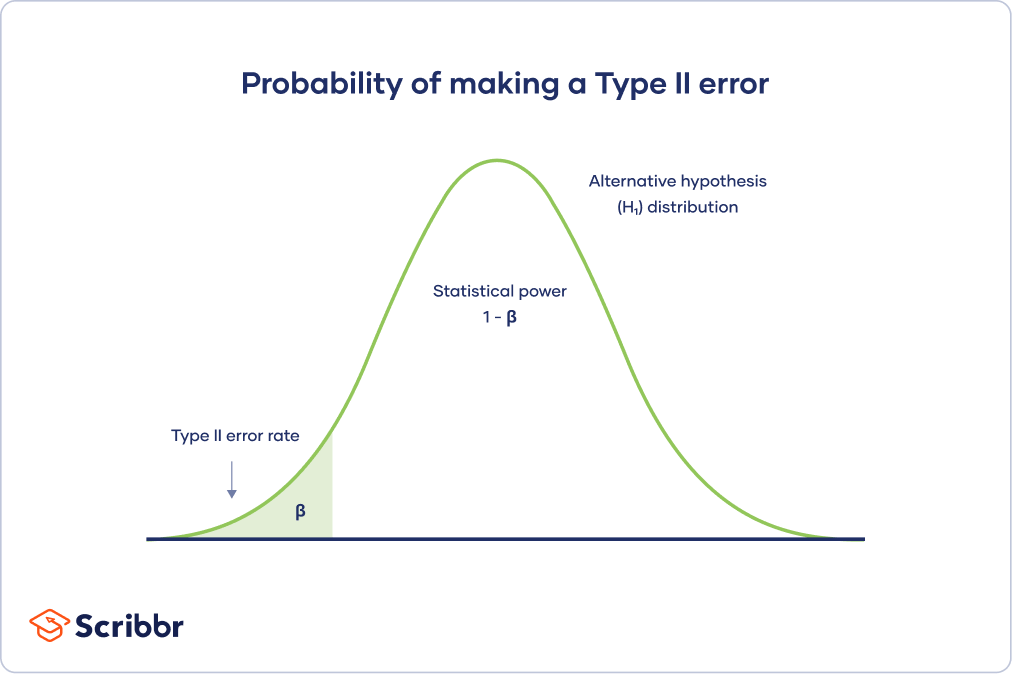
Traditionally, the corresponding Type I error rate is defined with a 5% significance level. Experiments are often designed to achieve some 80% throughput using a performance query. Note that the test determines whether statistical power can be determined.
Type II error is also known as false very bad. Type II error is inversely related to the characteristics associated with a statistical test. This means that the better the performance of the write test, the less likely it is to make a Type II error.
The performance is highly dependent on the characteristics of the sample (N). With a larger N, they are more likely to reject this null hypothesis if it is indeed false. As N increases, the generalized error decreases.