Table of Contents
Approved
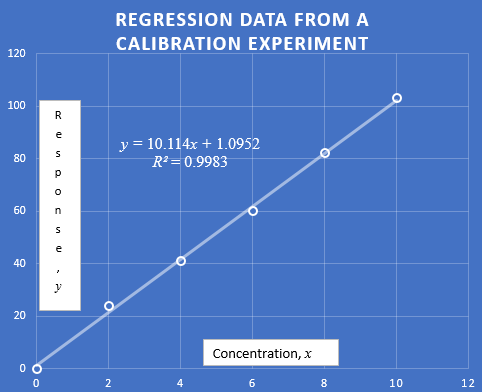
Here are a few simple methods that can help solve the problem of calibration curve error sources. Answer: A standard curve is an actual plot of an analytical signal (eg absorbance using absorbance spectrophotometry) versus concentration obtained from standard solutions. Thus, the real sources of errors are errors in the concentrations of standards and some errors in their measured signals.
Answer: A calibration curve can be a plot of analytical acceptance (eg absorbance in absorption spectrophotometry) versus the concentration of standard solutions. Thus, these main sources of error are errors in the standard concentrations along with errors in their estimated signals.
Standard Curve Method Using Linear Curve Fitting
First set mo=2, Space = 0, Ev and Es = 0 and set z = 0, n = 0, Cx = 5 and Cs = 10. Now increase the total non-linearity (variable “n”) leads to a clear non-linearity. How the analytical curve becomes more rounded, you can clearly see In particular, the least squares method no longer describes the curve well. Also, see R2 which is 1000 for the important ideal Straight, start to gradually fall, but R2 still shows 0.99 when The curve is already highly non-linear and already has a corresponding error of course, it began to degrade (see the error in the statistics table). exactly about 7% error. The even value of R2 is 0.999. error 2%. Maybe 2% sounds good and that’s why some in apps This may be necessary, but analytical methods are sometimes mentioned. to make measurements accurate to 0.1% or even better.To this shows us that R2 must end with multiple as specified (3 or maybe 4) decimals for analytical calibration purposes. Also try this simulation by default (variables “z” and “empty”); unfortunately you will see really no better than the only standard method that takes this into account. Set And ev Es=1 to provide a little random error.
The accuracy of some methods can be improved by adding an appropriate internal standard that references both calibration and biological standards.test samples, and basing a regression on the response coefficients of all analytes to help you with your internal standard. The use of an internal standard corrects small inconsistencies in operating conditions.
I. Introduction
Comparison of measurement results of completely different optical parameters shows significant differences in accuracy. There is no problem converting refractive indices to different decimal places, and the corrected spectrum tables give wavelengths between 6 and 7 significant figures. On the other hand, the actual permeability of an object can only be reported with an accuracy of 0.1%, and even this allows one to make statements only about random errors, but not about systematic errors.
These and many other similar tests have been and are still being performed along with solutions with multiple extended communication highs and lows. As a reference to the photometric and wavelength accuracy of real instruments, measurement wavelengths are sometimes given for extrema and to view the slopes of alarm curves, although such derivation should often not be possible. However, the author would also like to provide separate tests for wavelength accuracy and photometric accuracy for normal routine work. Only then will it be possible sometimes not only to experimentally prove the unreliability of the data, but also to obtain quantitative data suitable for correcting the results. Separate burial sourcesErrors are, of course, considered separately and eliminated when instruments and devices are likely to be tested in laboratories issuing calibration standards.
The software to fix your PC is just a click away - download it now.